Bab ini akan menerangkan bagaimana mengorganisasikan data dengan membentuk distribusi frekuensi dan bagaimana mengkonstruksi data dalam bentuk grafik dan diagram yang sesuai dengan tipe data sehingga mudah dipahami.
Istilah-istilah dasar:
1. Ketika data dikumpulkan dalam bentuk aslinya maka disebut sebagai raw data (data mentah).
2. Distribusi frekuensi adalah pengorganisasian data mentah dalam bentuk tabel, menggunakan kelas-kelas dan frekuensi-frekuensi.
3. Dua jenis distribusi yang dikenal luas adalah distribusi frekuensi kategori (categorical distribution frequency) dan distribusi frekuensi dalam group (grouped frequency distribution)
Manfaat Distribusi Frekuensi
– Untuk mengorganisasikan data menjadi lebih bermakna dan mudah dipahami.
– Agar memudahkan pembaca dalam membandingkan set data.
– Memudahkan dalam perhitungan ukuran rata-rata dan penyebaran data
– Untuk memdudahkan pembaca dalam menentukan bentuk distribusi data
– Memudahkan peneliti dalam menampilkan data dalam bentuk tabel dan grafik
Jenis-jenis Distribusi Frekuensi
A. Distribusi Frekuensi Kategori
Distribusi frekuensi kategori adalah digunakan untuk data kategorik seperti data nominal dan data ordinal. Seperti data kelompok jenis kelamin, kelompok jurusan atau kelompok status sosial ekonomi.
B. Distribusi Frekuensi Dalam Group
Distribusi Frekuensi Dalam Group digunakan untuk mengorganisasikan data numerik yang besar, sehingga perlu dikelompokkan ke dalam kelas dan frekuensi-frekuensi agar mudah dipahami.
Misalnya kita memiliki sekelompok data mengenai usia mahasiswa di salah satu jurusan berikut merupakan datanya: 18, 19. 19, 18, 21, 20, 20, 20, 19, 18, 18, 19, 21, 20, 23, 17
Bagaimana mengorganisasikan data di atas dalam bentuk distribusi frekuensi
Berikut merupakan langkah-langkahnya
1. Terntukan rentang data dengan mengurangkan nilai maksimum dikurangi nilai minimum.
2. Tentukan jumlah kelas yang paling mendekati dengan mengikuti aturan sturges
K = 1 + 3,3 log n
dimana k adalah jumlah kelas dan n adalah jumlah jumlah observasi
3. Tentukan panjang interval kelas
4. Tentukan batas kelas atas dahn batas kelas bawa
5. Masukan data ke dalam kelas yang telah dibentuk
Jenis Grafik dan Kegunaan
1. Histogram, Poligon dan Ogiv cocok digunakan ketika data telah disusun dalam bentuk distribusi frekuensi dalam group.
2. Diagram Pareto cocok digunakan untuk data nominal yang telah disusun dalam bentuk frekuensi.
3. Grafik Time series digunakan untuk menggambarkan pola dan trend data dari waktu ke waktu.
4. diagram Pie digunakan untuk menggambarkan hubungan diantara beberapa bagian secara keseluruhan.


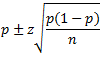

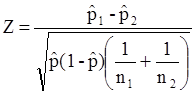
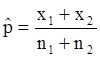

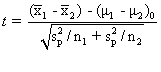
 tidak diketahui or dengan ukuran sampel n < 30.
tidak diketahui or dengan ukuran sampel n < 30.


